Finite Element Method (A Numerical approach to Problem Solving)

A Finite Element Method for Solving numerical problems

Image Source - https://pinterest.com/pin/445012006922298354/?source_app=android

Category :Programming

This article gives an introduction to Finite Element Method. Finite element method (FEM) is a numerical approach to solution of engineering problems involved in the field of Structural Mechanics, Thermal, Electrical and Electronics engineering field. Being a numerical solution it idealise the physical problem in numerical form and generates an approximate solution to the problem.

Finite Element Method (A Numerical approach to Problem Solving)

The method is extensively used by researchers and mathematicians to find the solution of various real life problems.

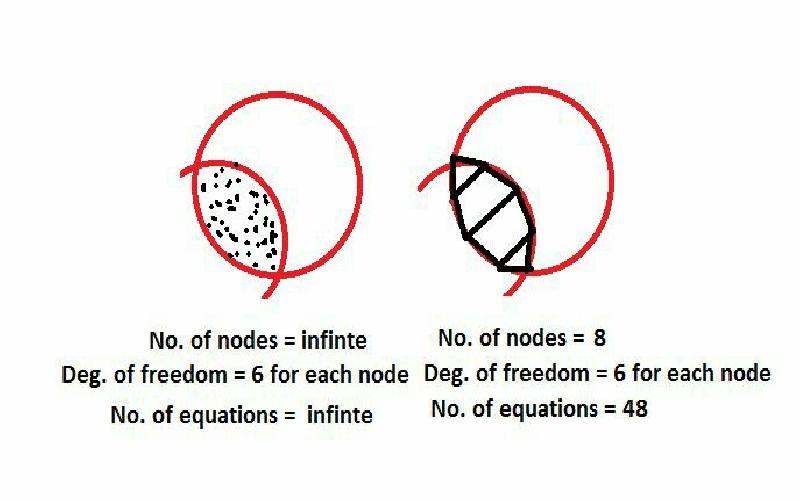
Finite element method is used for finding approximate solution to a problem by utilizing the numerical technique. It solves a boundary value problem for a partial differential equation by the method of discretization. The domain of the problem is divided in small parts or elements on which the equations involving the physics of the problem are applied. The variational methods are used to find the variation of the field parameters inside the elements. This division of the overall problem in to small parts is known as meshing.

The division of the overall problem domain in to small parts or elements has several advantages:

A more complex geometry can be covered by the process of meshing.
It can account for different materials at different locations or more broadly material change.
It can capture the discontinuities involved at several locations in the problem domain.

A lot of finite element solution software packages are available which have inbuilt solvers to make all the numerical computations and provides the results to any problem modelled in it. The most common and most reputed software for the Finite element method is ANSYS.

With the help of this software, solution to various problems in the field of structural mechanics, thermal engineering, vibration engineering and many more can be determined by finding out the approximate numerical solution of the problem involved.

The working sequence in the FEM software involves the modelling of the problem geometry in 2D (two dimensional) or 3D (three dimensional) mode with the help of any solid modelling software like CREO, SOLIDWORKS or CATIA. The model is then imported to the ANSYS environment. The next step is meshing or division of the CAD model in to number of elements. Then the boundary conditions and loads are applied according to the problem which needs to be investigated. The DOF (degree of freedom) constraints are then applied and the problem is simulated or solved. The plots or numerical values of the required results like stress distribution, temperature distribution etc can be found out.

Some other numerical methods are also being used apart from finite element method in numerical techniques like Finite Difference Method (FDM), which is also used for solving partial differential equations. In this a finite difference term is repeated over the whole domain. Besides these the Finite volume methods (FVM) are used to solve the problems involving fluid flow. This field is known as Computational fluid dynamics (CFD). In this case the region or the volume where there is a fluid flow involved is divided in small regions or finite volumes. The law and physics of fluid engineering are then applied to the system.

Thus Finite Element Method is a technique extensively used to simulate the various problems involved in the physical world and can anticipate the performance of the system in the real life conditions.